If you're a night owl like me you may have come across those late night game shows where you call in to win money. I'm not a fan of them. The rules are very vague, and they're broadcast on channel 74 (4ME) at a highly compressed resolution at 576i, so it can be hard to see some of the details (especially for older people). You've got to hand it to the hosts though, there's no way I couldn't stand there for hours babbling on a about nothing, that's what I have a blog for :-)
One of the games they've been playing lately intrigued me. You have to find all the triangles in a diagram like the one below, and then add all the numbers in each triangle together to reach a final value.
 |
| Puzzle from Call and Win 15/12/2015 |
The host suggests a way to find the answer by drawing it out and finding all the triangles manually, and sure it'll work, but where's the fun in that I ask you? Can we write software to find the answer? Of course we can.
We'll start by taking a closer look at the puzzle. They use a mix of Roman and Arabic numeral to be "tricky". There are also some areas with multiple number in them. For our analysis these will be simplified manually when the problem is defined in software.
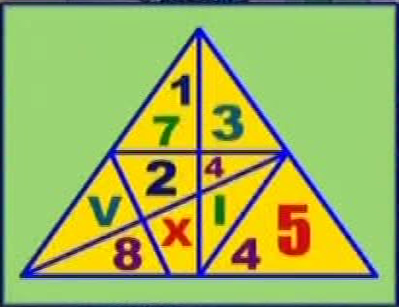 |
| Puzzle |
To start with, let's strip all the useless information and number each vertex. Each region will also be labelled with a number and its value placed in brackets. Now we can discuss the problem in formal terms.
To define the puzzle in terms that software can understand, it isn't sufficient to just feed it a list of vertices and how they're connected. For example, in the image below, if vertex 5 is moved into region 8. The connections of the graph are preserved, but its shape is changed. To make sure that the structure is well defined, it's better to define the network by describing each region by a list of vertices in a consistent clockwise or anticlockwise manner. This isn't exactly true, but it works for this problem. (I've had a crash course in graph theory and discovered and learnt some interesting things) That's great, but you can't find triangles with just a definition of the regions. A graph isn't a geometric representation of a structure, it just defines connections. Adding a list of the straight lines in the graph will enable us to solve the problem. These are defined by listing all groups of 3 or more vertices that are collinear (2 vertices are trivially collinear so they don't need to be defined).
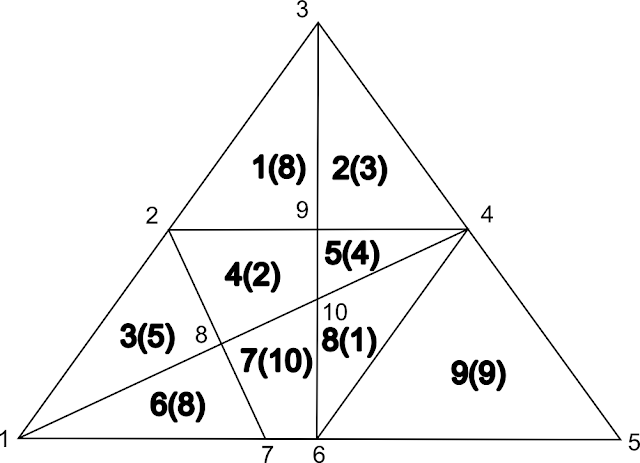 |
| Structured Network |
The above structured network (I'm calling it that because it's a network, but it has some geometric constraints) can be defined by the following 16 lines of code. The Region objects are defined by supplying an id, a value, and a list of vertices. The StraightLineSegment objects are defined by a set of vertices.
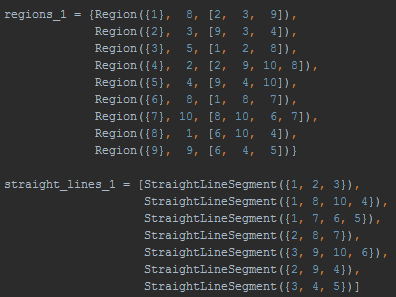 |
| Defining the structured network |
We now have the network defined in software, but how do we actually solve the problem? The human way to go about it is to find the triangles and then add all the numbers in them. It's trivial to write a program to find the triangles in the network. For example pick, vertex 1, it's connected by straight lines to vertices 2, 3, 8, 10, 4, 7, 6, 5. For each of these vertices you would then repeat the process. Let's choose vertex 2. It's connected to vertices (1, 8, 7, 9, 4, 3) by straight lines. You ignore vertex 1 because that's where you came from, but if any of these vertices can be connected back to vertex 1, you've found a triangle. Out of that last list, vertices (8, 7, 4, 3) connect to vertex 1. This means you've found 3 triangles, (1,2,8), (1,2,7), (1,2,4). You ignore vertex 3 because it's a straight line. There's a subtle problem with that though. It's hard to find the regions that make up a compound region like the one constrained by the vertices (1, 2, 4). This means it's hard to add the numbers together. It's easy for humans, but it's not as simple for computers.
The way I've chosen to solve the problem is to find every possible compound region in the network adding the values as I go. The triangular regions are then identified and the others are discarded.
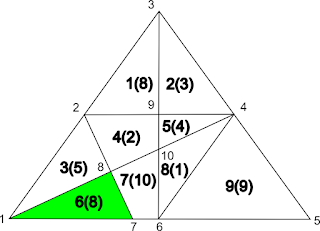 |
| Finding compound regions |
You may be thinking "Oh, it's just combinations of regions", but hold on. If I want the region that's a combination of regions 6, 7, and 8. You need to know how to construct it. (Region 6 + Region 7) + Region 8 makes sense, but (Region 6 + Region 8) + Region 7 doesn't. Adding Region 6 to 8 doesn't make sense they aren't connected. This implies that Region addition isn't commutative.
The easiest way to find all compound regions is to start with all the base regions and see how many regions with two base regions you can find. For example if we select region 6. It's connected to regions 3 and 7.
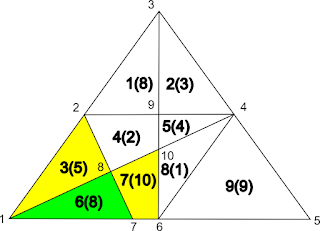 |
| Expanding a region |
This means you've found two regions with 2 base regions. The new regions are region {6, 3} and region {6, 7}. Because they've been discovered by looking at connected regions it's easy to find the vertices that describe their edges. It's also easy to add their values.
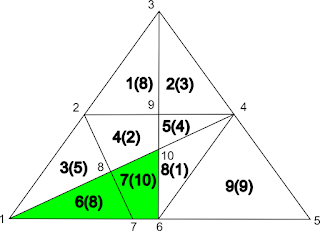 |
| Compound region {6,7} |
You'll find duplicate regions using this method, but they're easily removed. Once you've found all the compound regions with 2 base regions in them, you can repeat the process to find all the regions with 3 base regions in them. For example if region {6, 7} is chosen, you can see that 3 new regions {3, 6, 7} {4, 6, 7} and {6, 7, 8} are found. This process is repeated until you find a region that contains all base regions. Once this point is reached, there are no more regions to add.
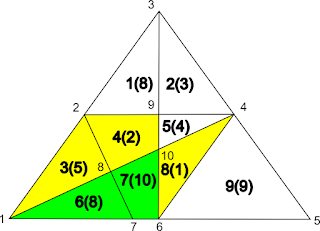 |
| Expanding region {6,7} |
Now triangles need to be identified. Let's look at region {6, 7, 8}. It's defined by a vertex list of [1, 8, 10, 4, 6, 7]. If we look at this ordered circular list 3 vertices at a time we can find vertices to remove. For example vertices [1, 8 ,10] are collinear. This means we can remove vertex 8 from the list. Repeating this process until no more vertices can be removed will show if the region is triangular.
For example
[1, 8, 10, 4, 6, 7] -> [1, 10, 4, 6, 7] -> [1, 4, 6, 7] -> [1, 4, 6]
You now have a list containing 3 vertices. This means it's a triangle. You then just go through and find the sum of all these elements. I'll go into some more of the theory and implementation in the next blog post, but that's the basics of it.
If you've read this far I bet you've tried to work out the answer. Scroll to the bottom of this page and you can see the output of my program with the answer way down the bottom
 |
| Get the code! |
Base regions ({id} =value= *vertices*)
count = 9
({7} =10= *10* *6* *7* *8*)
({5} =4= *9* *4* *10*)
({3} =5= *1* *2* *8*)
({6} =8= *1* *8* *7*)
({8} =1= *6* *10* *4*)
({4} =2= *10* *8* *2* *9*)
({1} =8= *2* *3* *9*)
({2} =3= *4* *9* *3*)
({9} =9= *5* *6* *4*)
Multi edge straight lines -*vertices*-
count = 7
-*1* *2* *3*-
-*8* *1* *10* *4*-
-*1* *5* *6* *7*-
-*8* *2* *7*-
-*9* *10* *3* *6*-
-*9* *2* *4*-
-*3* *4* *5*-
edge list |*vertices*| -> {connected region id}
count = 18
|*9* *2*| -> {4}{1}
|*10* *6*| -> {7}{8}
|*9* *4*| -> {5}{2}
|*1* *7*| -> {6}
|*3* *4*| -> {2}
|*8* *1*| -> {6}{3}
|*1* *2*| -> {3}
|*6* *7*| -> {7}
|*8* *2*| -> {4}{3}
|*9* *3*| -> {2}{1}
|*8* *7*| -> {6}{7}
|*2* *3*| -> {1}
|*8* *10*| -> {7}{4}
|*4* *6*| -> {8}{9}
|*5* *6*| -> {9}
|*10* *4*| -> {5}{8}
|*9* *10*| -> {4}{5}
|*4* *5*| -> {9}
Compound regions ({id} =value= *vertices*)
count = 174
({4, 6, 7} =20= *6* *7* *1* *8* *2* *9* *10*)
({6, 7} =18= *10* *6* *7* *1* *8*)
({1, 2, 4, 5, 7, 8, 9} =37= *3* *4* *5* *6* *7* *8* *2*)
({1, 4, 7} =20= *2* *3* *9* *10* *6* *7* *8*)
({8, 9} =10= *5* *6* *10* *4*)
({8, 1, 4, 5, 7} =25= *4* *6* *7* *8* *2* *3* *9*)
({1, 2, 3, 4, 5, 6, 8} =31= *1* *2* *3* *4* *6* *10* *8* *7*)
({2, 3, 4, 5, 6, 8} =23= *1* *2* *9* *3* *4* *6* *10* *8* *7*)
({1, 3, 4, 7, 8, 9} =35= *1* *2* *3* *9* *10* *4* *5* *6* *7* *8*)
({1, 3, 4, 5, 7} =29= *4* *10* *6* *7* *8* *1* *2* *3* *9*)
({1, 4, 5, 6, 7, 8} =33= *3* *9* *4* *6* *7* *1* *8* *2*)
({5} =4= *9* *4* *10*)
({1, 3, 4, 6, 7, 8, 9} =43= *5* *6* *7* *1* *2* *3* *9* *10* *4*)
({2, 5, 6, 7, 8, 9} =35= *4* *5* *6* *7* *1* *8* *10* *9* *3*)
({3, 4} =7= *1* *2* *9* *10* *8*)
({8, 9, 6, 7} =28= *5* *6* *7* *1* *8* *10* *4*)
({2, 5} =7= *4* *10* *9* *3*)
({8, 4, 7} =13= *6* *7* *8* *2* *9* *10* *4*)
({1, 4, 5, 7} =24= *6* *7* *8* *2* *3* *9* *4* *10*)
({1, 2, 3, 4, 7, 8, 9} =38= *5* *6* *7* *8* *1* *2* *3* *4* *9* *10* *4*)
({8, 9, 4, 5} =16= *4* *5* *6* *10* *8* *2* *9*)
({8, 9, 4, 5, 1} =24= *4* *5* *6* *10* *8* *2* *3* *9*)
({1, 4, 5, 6, 7} =32= *6* *7* *1* *8* *2* *3* *9* *4* *10*)
({2, 3, 4, 5, 7} =24= *4* *10* *6* *7* *8* *1* *2* *9* *3*)
({1, 3, 4, 6, 7, 8} =34= *7* *1* *2* *3* *9* *10* *4* *6*)
({1, 3, 4} =15= *2* *3* *9* *10* *8* *1*)
({8, 5} =5= *9* *4* *6* *10*)
({1, 2, 5, 6, 7, 8} =34= *3* *4* *6* *7* *1* *8* *10* *9* *2*)
({2, 3, 4, 5, 6} =22= *4* *10* *8* *7* *1* *2* *9* *3*)
({8, 1, 2, 4, 5} =18= *8* *2* *3* *4* *6* *10*)
({8, 3, 4, 5, 6} =20= *1* *2* *9* *4* *6* *10* *8* *7*)
({3, 4, 5} =11= *8* *1* *2* *9* *4* *10*)
({2, 3, 5, 6, 7, 8} =31= *9* *3* *4* *6* *7* *1* *2* *8* *10*)
({8, 1, 4, 5} =15= *8* *2* *3* *9* *4* *6* *10*)
({1, 3, 4, 7} =25= *10* *6* *7* *8* *1* *2* *3* *9*)
({3, 4, 5, 7, 8, 9} =31= *5* *6* *7* *8* *1* *2* *9* *4*)
({6} =8= *1* *8* *7*)
({8, 4, 5, 7} =17= *9* *4* *6* *7* *8* *2*)
({8, 9, 5} =14= *5* *6* *10* *9* *4*)
({8, 2, 5} =8= *4* *6* *10* *9* *3*)
({8, 2, 3, 4, 5} =15= *8* *1* *2* *9* *3* *4* *6* *10*)
({1} =8= *2* *3* *9*)
({1, 2, 3, 4, 5, 6, 7, 8} =41= *7* *1* *2* *3* *4* *6*)
({2, 3, 4, 5, 6, 8, 9} =32= *4* *5* *6* *10* *8* *7* *1* *2* *9* *3*)
({3, 4, 5, 7} =21= *1* *2* *9* *4* *10* *6* *7* *8*)
({8, 9, 2, 4, 5} =19= *4* *5* *6* *10* *8* *2* *9* *3*)
({2, 4, 5, 7} =19= *4* *10* *6* *7* *8* *2* *9* *3*)
({4, 7} =12= *6* *7* *8* *2* *9* *10*)
({1, 2, 5, 6, 7, 8, 9} =43= *3* *4* *5* *6* *7* *1* *8* *10* *9* *2*)
({2, 3, 4, 5} =14= *4* *10* *8* *1* *2* *9* *3*)
({9} =9= *5* *6* *4*)
({1, 4, 6, 7, 8, 9} =38= *3* *9* *10* *4* *5* *6* *7* *1* *8* *2*)
({4, 5, 6, 7} =24= *6* *7* *1* *8* *2* *9* *4* *10*)
({8, 5, 7} =15= *6* *7* *8* *10* *9* *4*)
({1, 2, 3, 4, 5, 6, 7, 8, 9} =50= *1* *2* *3* *4* *5* *6* *7*)
({8, 1, 3, 4, 5} =20= *8* *1* *2* *3* *9* *4* *6* *10*)
({2} =3= *4* *9* *3*)
({8, 9, 5, 7} =24= *5* *6* *7* *8* *10* *9* *4*)
({1, 2, 4, 6, 7, 8} =32= *3* *4* *9* *10* *4* *6* *7* *1* *8* *2*)
({3, 4, 6} =15= *1* *2* *9* *10* *8* *7*)
({3, 4, 7} =17= *1* *2* *9* *10* *6* *7* *8*)
({1, 2, 4, 5, 8, 9} =27= *8* *2* *3* *4* *5* *6* *10*)
({2, 4, 5, 6, 7, 8, 9} =37= *4* *5* *6* *7* *1* *8* *2* *9* *3*)
({1, 3, 4, 5, 7, 8, 9} =39= *4* *5* *6* *7* *8* *1* *2* *3* *9*)
({3, 4, 5, 6} =19= *8* *7* *1* *2* *9* *4* *10*)
({1, 3, 4, 5, 6, 7} =37= *6* *7* *1* *2* *3* *9* *4* *10*)
({8, 9, 2, 5, 1} =25= *3* *4* *5* *6* *10* *9* *2*)
({1, 2, 4, 5, 6, 7, 8} =36= *3* *4* *6* *7* *1* *8* *2*)
({3, 5, 6, 7, 8, 9} =37= *9* *4* *5* *6* *7* *1* *2* *8* *10*)
({8, 9, 3, 6, 7} =33= *4* *5* *6* *7* *1* *2* *8* *10*)
({1, 2, 5, 7, 8, 9} =35= *3* *4* *5* *6* *7* *8* *10* *9* *2*)
({1, 2, 4, 6, 7, 8, 9} =41= *5* *6* *7* *1* *8* *2* *3* *4* *9* *10* *4*)
({1, 2, 3, 4, 6, 7, 8, 9} =46= *5* *6* *7* *1* *2* *3* *4* *9* *10* *4*)
({8, 1, 4, 6, 7} =29= *7* *1* *8* *2* *3* *9* *10* *4* *6*)
({1, 4} =10= *10* *8* *2* *3* *9*)
({2, 4, 5, 6, 7} =27= *4* *10* *6* *7* *1* *8* *2* *9* *3*)
({1, 2, 4, 5, 7} =27= *2* *3* *4* *10* *6* *7* *8*)
({3, 4, 5, 6, 7} =29= *6* *7* *1* *2* *9* *4* *10*)
({1, 2, 4, 7, 8, 9} =33= *5* *6* *7* *8* *2* *3* *4* *9* *10* *4*)
({3, 4, 6, 7, 8, 9} =35= *5* *6* *7* *1* *2* *9* *10* *4*)
({4, 5, 7} =16= *6* *7* *8* *2* *9* *4* *10*)
({3, 4, 5, 6, 7, 8} =30= *7* *1* *2* *9* *4* *6*)
({8, 1, 2, 4, 7} =24= *6* *7* *8* *2* *3* *4* *9* *10* *4*)
({1, 2, 3, 4, 6, 7} =36= *6* *7* *1* *2* *3* *4* *9* *10*)
({8, 2, 5, 6, 7} =26= *4* *6* *7* *1* *8* *10* *9* *3*)
({8, 1, 2, 5} =16= *3* *4* *6* *10* *9* *2*)
({8, 6, 7} =19= *7* *1* *8* *10* *4* *6*)
({1, 2, 3, 5, 6, 7, 8, 9} =48= *3* *4* *5* *6* *7* *1* *2* *8* *10* *9* *2*)
({8, 3, 5, 6, 7} =28= *9* *4* *6* *7* *1* *2* *8* *10*)
({8, 1, 3, 4, 7} =26= *1* *2* *3* *9* *10* *4* *6* *7* *8*)
({2, 4, 5, 6, 7, 8} =28= *7* *1* *8* *2* *9* *3* *4* *6*)
({1, 3, 4, 5, 7, 8} =30= *1* *2* *3* *9* *4* *6* *7* *8*)
({2, 3, 5, 6, 7, 8, 9} =40= *9* *3* *4* *5* *6* *7* *1* *2* *8* *10*)
({1, 2, 4, 5, 6, 7, 8, 9} =45= *3* *4* *5* *6* *7* *1* *8* *2*)
({8, 9, 4, 7} =22= *5* *6* *7* *8* *2* *9* *10* *4*)
({1, 2, 3, 4, 5, 8, 9} =32= *2* *3* *4* *5* *6* *10* *8* *1*)
({8, 2, 4, 5} =10= *4* *6* *10* *8* *2* *9* *3*)
({3} =5= *1* *2* *8*)
({8, 3, 4, 5, 7} =22= *6* *7* *8* *1* *2* *9* *4*)
({2, 3, 4, 5, 7, 8, 9} =34= *1* *2* *9* *3* *4* *5* *6* *7* *8*)
({1, 2, 4, 5, 6, 7} =35= *3* *4* *10* *6* *7* *1* *8* *2*)
({1, 3, 4, 5, 6, 8, 9} =37= *4* *5* *6* *10* *8* *7* *1* *2* *3* *9*)
({8, 9, 2, 5, 7} =27= *3* *4* *5* *6* *7* *8* *10* *9*)
({8, 3, 4, 5} =12= *8* *1* *2* *9* *4* *6* *10*)
({8, 9, 3, 4, 7} =27= *1* *2* *9* *10* *4* *5* *6* *7* *8*)
({2, 3, 4, 5, 6, 7, 8, 9} =42= *4* *5* *6* *7* *1* *2* *9* *3*)
({8, 9, 2, 5} =17= *4* *5* *6* *10* *9* *3*)
({1, 3, 4, 5, 8, 9} =29= *4* *5* *6* *10* *8* *1* *2* *3* *9*)
({1, 2, 3, 4, 5, 6, 8, 9} =40= *1* *2* *3* *4* *5* *6* *10* *8* *7*)
({1, 3, 4, 5, 6, 7, 8, 9} =47= *4* *5* *6* *7* *1* *2* *3* *9*)
({1, 3, 4, 6, 7} =33= *7* *1* *2* *3* *9* *10* *6*)
({1, 3, 4, 5, 6} =27= *4* *10* *8* *7* *1* *2* *3* *9*)
({8, 4, 6, 7} =21= *7* *1* *8* *2* *9* *10* *4* *6*)
({1, 4, 5} =14= *8* *2* *3* *9* *4* *10*)
({2, 3, 4, 5, 7, 8} =25= *4* *6* *7* *8* *1* *2* *9* *3*)
({1, 2, 3, 4, 5, 7, 8} =33= *1* *2* *3* *4* *6* *7* *8*)
({1, 3, 4, 5} =19= *4* *10* *8* *1* *2* *3* *9*)
({8, 9, 3, 4, 5} =21= *2* *9* *4* *5* *6* *10* *8* *1*)
({1, 3, 4, 5, 6, 7, 8} =38= *7* *1* *2* *3* *9* *4* *6*)
({8, 9, 4, 5, 7} =26= *9* *4* *5* *6* *7* *8* *2*)
({8, 3, 4, 7} =18= *7* *8* *1* *2* *9* *10* *4* *6*)
({8, 7} =11= *7* *8* *10* *4* *6*)
({3, 6, 7} =23= *7* *1* *2* *8* *10* *6*)
({1, 3, 4, 5, 6, 8} =28= *1* *2* *3* *9* *4* *6* *10* *8* *7*)
({3, 4, 5, 6, 7, 8, 9} =39= *5* *6* *7* *1* *2* *9* *4*)
({2, 4, 5} =9= *4* *10* *8* *2* *9* *3*)
({8, 9, 7} =20= *4* *5* *6* *7* *8* *10*)
({8, 9, 7, 4, 1} =30= *10* *4* *5* *6* *7* *8* *2* *3* *9*)
({1, 2, 3, 4, 5, 6, 7} =40= *6* *7* *1* *2* *3* *4* *10*)
({3, 6} =13= *1* *2* *8* *7*)
({1, 2, 3, 4} =18= *2* *3* *4* *9* *10* *8* *1*)
({1, 2} =11= *2* *3* *4* *9*)
({8, 4, 5} =7= *4* *6* *10* *8* *2* *9*)
({1, 2, 4} =13= *8* *2* *3* *4* *9* *10*)
({1, 4, 6, 7} =28= *10* *6* *7* *1* *8* *2* *3* *9*)
({8, 9, 4, 6, 7} =30= *9* *10* *4* *5* *6* *7* *1* *8* *2*)
({1, 2, 3, 4, 6} =26= *8* *7* *1* *2* *3* *4* *9* *10*)
({1, 2, 3, 4, 5, 6} =30= *1* *2* *3* *4* *10* *8* *7*)
({1, 2, 4, 6, 7} =31= *6* *7* *1* *8* *2* *3* *4* *9* *10*)
({3, 4, 5, 6, 8, 9} =29= *1* *2* *9* *4* *5* *6* *10* *8* *7*)
({1, 3, 4, 6} =23= *10* *8* *7* *1* *2* *3* *9*)
({7} =10= *10* *6* *7* *8*)
({2, 4, 5, 7, 8, 9} =29= *4* *5* *6* *7* *8* *2* *9* *3*)
({1, 2, 4, 7} =23= *6* *7* *8* *2* *3* *4* *9* *10*)
({3, 4, 6, 7} =25= *10* *6* *7* *1* *2* *9*)
({1, 2, 3, 4, 6, 7, 8} =37= *7* *1* *2* *3* *4* *9* *10* *4* *6*)
({1, 2, 4, 5} =17= *3* *4* *10* *8* *2*)
({1, 2, 3, 4, 5} =22= *2* *3* *4* *10* *8* *1*)
({2, 3, 4, 5, 6, 7, 8} =33= *7* *1* *2* *9* *3* *4* *6*)
({8, 1, 4, 7} =21= *7* *8* *2* *3* *9* *10* *4* *6*)
({1, 2, 3, 4, 5, 8} =23= *8* *1* *2* *3* *4* *6* *10*)
({8, 5, 6, 7} =23= *6* *7* *1* *8* *10* *9* *4*)
({1, 2, 4, 5, 7, 8} =28= *3* *4* *6* *7* *8* *2*)
({8, 3, 4, 6, 7} =26= *7* *1* *2* *9* *10* *4* *6*)
({8} =1= *6* *10* *4*)
({1, 2, 3, 4, 5, 7, 8, 9} =42= *1* *2* *3* *4* *5* *6* *7* *8*)
({1, 2, 3, 5, 6, 7, 8} =39= *3* *4* *6* *7* *1* *2* *8* *10* *9* *2*)
({8, 2, 5, 7} =18= *3* *4* *6* *7* *8* *10* *9*)
({8, 1, 2, 5, 7} =26= *3* *4* *6* *7* *8* *10* *9* *2*)
({8, 9, 5, 6, 7} =32= *5* *6* *7* *1* *8* *10* *9* *4*)
({1, 4, 5, 7, 8, 9} =34= *3* *9* *4* *5* *6* *7* *8* *2*)
({8, 2, 4, 5, 7} =20= *7* *8* *2* *9* *3* *4* *6*)
({2, 3, 4, 5, 6, 7} =32= *4* *10* *6* *7* *1* *2* *9* *3*)
({4} =2= *10* *8* *2* *9*)
({1, 2, 5} =15= *3* *4* *10* *9* *2*)
({2, 3, 4, 5, 8, 9} =24= *2* *9* *3* *4* *5* *6* *10* *8* *1*)
({1, 2, 3, 4, 5, 7} =32= *1* *2* *3* *4* *10* *6* *7* *8*)
({1, 2, 3, 4, 7} =28= *1* *2* *3* *4* *9* *10* *6* *7* *8*)
({4, 5, 6, 7, 8, 9} =34= *9* *4* *5* *6* *7* *1* *8* *2*)
({1, 4, 5, 6, 7, 8, 9} =42= *4* *5* *6* *7* *1* *8* *2* *3* *9*)
({8, 3, 6, 7} =24= *4* *6* *7* *1* *2* *8* *10*)
({1, 2, 3, 4, 7, 8} =29= *1* *2* *3* *4* *9* *10* *4* *6* *7* *8*)
({8, 4, 5, 6, 7} =25= *6* *7* *1* *8* *2* *9* *4*)
({4, 5} =6= *4* *10* *8* *2* *9*)
Triangular Regions ({id} =value= *vertices*)
count = 22
({8, 6, 7} =19= *7* *1* *8* *10* *4* *6*)
({3, 6} =13= *1* *2* *8* *7*)
({1, 2} =11= *2* *3* *4* *9*)
({6, 7} =18= *10* *6* *7* *1* *8*)
({1, 2, 3, 4, 5} =22= *2* *3* *4* *10* *8* *1*)
({5} =4= *9* *4* *10*)
({3} =5= *1* *2* *8*)
({8, 9, 6, 7} =28= *5* *6* *7* *1* *8* *10* *4*)
({2, 5} =7= *4* *10* *9* *3*)
({9} =9= *5* *6* *4*)
({2} =3= *4* *9* *3*)
({8, 9, 2, 5} =17= *4* *5* *6* *10* *9* *3*)
({1, 2, 3, 4, 5, 6, 7, 8, 9} =50= *1* *2* *3* *4* *5* *6* *7*)
({1, 3, 4, 6, 7} =33= *7* *1* *2* *3* *9* *10* *6*)
({8} =1= *6* *10* *4*)
({1, 3, 4} =15= *2* *3* *9* *10* *8* *1*)
({8, 5} =5= *9* *4* *6* *10*)
({8, 2, 5} =8= *4* *6* *10* *9* *3*)
({3, 4, 5} =11= *8* *1* *2* *9* *4* *10*)
({6} =8= *1* *8* *7*)
({1} =8= *2* *3* *9*)
({4, 5} =6= *4* *10* *8* *2* *9*)
Sum of all the numbers in each triangular region = 301

Fascinating!! I skimmed through it. But will reread in a moment. I too like these games, and started creating a program, in December 2015 to solve them. I left it idle for a while, then got back into it heavily. It's going really well now. I have a similar, but different approach to you. I label my vertices with letters (A, B, C...). I am programming it using MS QuickBASIC v4.5 (c) 1985-1988. And it works visually as well as logically and mathematically. I still have many minor bugs in it, and little features to add to it, like 'snap to line', for vertex placement, and automatic vertex discovery.
ReplyDeleteWhen you see a new puzzle, how do you enter it into your program?
How long does it take to enter in one, for example, the above one?
Thanks, from Joshua, in Sydney, Australia
Sorry it took me so long to reply. It sounds like your writing the part of the program I wish I had. A graphical interface for entering the data would be ideal, but at the moment I draw and label the diagram by hand, then enter the data into the source file manually. Depending on the complexity of the problem and how fast I am, it takes 10 to 20 minutes. I didn't do an interface because I was mainly interested in coming up with a reasonably efficient algorithm to solve the problem. Thanks for the interest and I hope your version goes well.
Delete