Generate an STL 3D model with a surface described by an equation

I recently needed to generate a 3D model for printing based on an equation and couldn't find software to do the job.  In the end the easiest thing to do was to write a quick Python script called "stl-surface.py" to do the job.

At first the task seemed daunting, but generating the STL file is rather easy with the use of the numpy-stl library. The equation for the surface is calculated over a structured square/rectangular grid and each little cell of the grid is split in two to form triangles. You use many many of these small triangular faces to construct the model. All you have to do is to generate the coordinates for the 3 vertices that make up each triangle and numpy-stl does the rest. The bottom and sides are flat which makes things rather easy, and the top is defined by the equation.

When constructing the model it's important to list the coordinates of each face in a counter clockwise direction when looking at the model from the outside. This allows numpy-stl to later calculate things like volume of the model and centre of gravity and also test if the surface is closed (although they use a slightly buggy way to test this).

I've shown a few examples of the generated models below.

10 - 2*(1 - math.cos(2 * x * math.pi / 20)) * (1 - math.cos(2 * y * math.pi / 20))

Dimpled 3D model

10 + 2 * math.cos(math.sqrt((x - 50)**2 + (y - 50)**2)/2)

Rippled 3D model

Here you can see how the triangles are assembled to construct the model.

The triangular faces that make up the model

The triangles that form the edges of the model

Edge of the model

From the top you can see the grid points where the surface function is evaluated.

Top of the model

I hope this code can help someone else. I may not be the easiest thing to use and if you need help getting started get in touch.

Get the code!

Self Normalising Price Markdowns For Short Life Products

When selling products that have a relatively short shelf life, it becomes necessary to reduce the price on items as they approach their use by date so they sell and aren't thrown out.  This is done for several reasons.

• Sending plastic packaging and food that's safe to eat to landfill is a waste of resources, and in 2019 we can do a lot better than that
• If a business can reduce its waste, they can save money on garbage collection
• It's an acknowledgement to customers that the product isn't as flexible as one with a longer use by date
• It adds a little excitement for customers if they can buy a product that they normally wouldn't buy because it's normally too expensive

In my experience, supermarkets perform markdowns in an incremental way to make sure that stock isn't wasted, and to get as much money for the product that is possible.  This was usually accomplished by reducing the price by 20% on the 2nd last day of sale, 30% on the morning of the last day of sale, 40% at lunch time on the last day of sale and then going 50%, 60%, 70%, 80%, and 90% until the close of the store.  In essence, it's a Dutch auction. This works well but has problems.  People buy the most popular items first leaving an assortment of unappealing products towards the end.  As fixed percentages are used across the board, it means you might be reducing some items more than you need to and some less than you need to.  It's also reasonably labour intensive.

If you track markdowns and plot a graph of the most common ones you end up with a graph like the one below, which I'll use to demonstrate a point.

Markdowns shouldn't waste time or money

In the graph above you can see that average markdown is around 50%.  Traditionally you'd start with a 20% markdown, but the graph shows that in this case almost no one will buy the product at that discount.  This is the "Waste of Time" section of the graph.  Most likely you'll have to come back and do another markdown on the product.  Conversely if you go straight to an 80% markdown you've wasted money because you mostly likely could have sold the product for more.  The "Waste of Money" section.  Ideally most of the markdowns should be in the 30% to 70% range, the "Sweet Spot". But how do you calculate the markdown percentages?

I'm going to demonstrate a method that doesn't necessarily generate optimum markdown percentages, but does generate percentages so that popular and unpopular products sell at roughly the same rate with a reasonable chance of selling on the first markdown.

Let's start with some Lamb Hearts, and to keep things simple, from most to least recent the markdown percentages are as follows, 98%, 66%, and 6%.  This process uses a method called Kernel Density Estimation to generate a smooth curve of markdown probabilities.  This means that at each of those percentages above you place a predefined shape, in this case a Gaussian distribution.

Initial placement of kernels

You can see the distributions listed above.  You may notice that because the grey and blue curves are truncated at the sides of the graph the area under them is less.  This means that they'll have less of an influence on the result.  This can be corrected with a simple scaling process though.

Compensation for truncated kernels

The areas under the graphs above are now all the same, but is this what we want?  Most recent markdowns should have a greater impact on the process than ones that were performed long ago.  To correct this, each peak is weighted by 3 for the most recent, 2 for the next most recent, and 1 for the oldest markdown.

Weighting the kernels for recency

Adding each of these graphs gives the final markdown distribution in yellow.

Summation of the kernels

Now we perform a process called integration to get the light blue line.  For those of you unfamiliar integration it basically records the area under a graph. For example at the 20 point on the bottom axis the blue line records the area under the yellow line up until that point.

Integration of the distribution to produce the final curve

The next step is to introduce the concept of a markdown level which ranges from 0 to 10.  0 corresponds to a 0% markdown and 10 corresponds to a 100% markdown, but in between, things are very different.  As a demonstration we'll calculate the markdown percentages for markdown levels 2, 5, and 8.  The process is quite simple.  Find the levels on the left hand side of the graph and project them across to the blue curve and then down to the bottom of the graph.  This gives percentages of 53, 80 and then 94.

Calculating markdowns percentages from the graph

For another demonstration let's try something popular like chicken breast that has recent markdowns of 30%, 10%, and 20%.  This leads to percentages of 10, 22, and 33.

Calculating markdowns percentages from the graph

Like I said above, this isn't designed to generate an optimum markdown, it's designed to create a markdown specific to each product so that they'll sell at similar rates.  In the demonstration above the situation may warrant a level 2 markdown.  This means that a product that's hard to sell like lamb hearts gets a 53% markdown, while a popular item like chicken breast only gets a 10% markdown.

So a strategy may be to use a level 2 markdown on the second last day of sale, and then taper throughout the trading day from level 3 to 10 on the last day.

The demonstrations above have been quite simple and don't give a full picture of how powerful this method can be.  Let's put together a complicated situation with fake data to test it.

A new flavour of sausages is introduced and we are unsure how they'll perform.  They initially use an assumed prior that isn't mentioned above, but it quickly becomes obvious that they are a good seller and don't require large markdowns, with the first level 2 markdown being in the region of 15%.  After 500 recorded markdowns a new similar cheaper line is introduced and the sales of the original line suffer.  Before long the system calculates that the first markdown at level 2 needs to be about 55%

Animation of the markdown calculation process

The animation above is generated from 500 random markdowns with an average of 20% and then 500 random markdowns with an average of 80%.  The calculations take into account the last 100 markdown and are weighted from 1 to 100.

There are a couple important points to consider.  Firstly the process uses a lot of statistical methods and equations but isn't really grounded in theory.  It uses the properties of the methods to create a stable system that fits the requirements that are specified. The next thing to remember is that this process will follow the markdowns.  If you start the markdown process at level 8 without even trying something less than a level 5.  The system will generate larger and larger markdowns.  A stabilising term can be added to prevent this.

It's not a perfect method but it's a lot better than some of the optimised markdown systems I've seen.  I actually trialed this process a while ago(I have no deep access to the computers and had to do it manually) in my store and it's fascinating to see it converge on higher and lower markdowns based on the saleability of the product.

Reducing Evaporation Rates With Rippled Surfaces

A theory that I want to test out is that adding a ripple to a surface makes it easier to clean in certain situations.  I work in retail, and sometimes the cleaning of non food safety related issues are delayed due to more important tasks.  In particular I'm talking about drips.  You might see these on metal trays under bottles of milk in the fridge, or on plastic sheets under the shelves in the meat department.  In both cases drips are meant to be caught on a surface that is easy to remove and clean.  The problem is that if you leave a spill too long it dries and become hard to remove and requires vigorous cleaning which may damage the surface and waste time.

To avoid this, you want to slow the rate of evaporation.  This can be done by decreasing the surface area by increasing the depth.  A rippled surface is perfect for this.  You essentially make little cups to hold the spill.  Another requirement that would be nice to include is no tight internal corners.  Anything that is designed to be cleaned shouldn't contain a concave surface that you can't get a finger into.  Anyone that knows me well understands that I think in equations, and the one below matches our criteria perfectly.

$$$z=10 - 8 \left(\dfrac{1-\cos(2\pi x / 20)}{2}\right)\left(\dfrac{1-\cos(2\pi y / 20)}{2}\right)$$$

Let's talk about what this equation means.  The two large sections in the brackets are periodic terms that create ripples in the x and y directions.  The 20 means that this ripple will repeat every 20mm.  By subtracting the cos term from one and then dividing that result by 2, the term in the bracket will range from 0 to 1.  Multiplying the two brackets together will also give a result between 0 and 1.  By multiplying this by 8 we now have a function that ranges from 0 to 8.  The 10 describes the maximum of the equation.  By subtracting the rest of the equation from 10 we now have a surface that ranges from 2 to 10 above zero.  The important things to remember are, 20 specifies how wide the ripples are, and 8 describes how deep they are.

Sometimes though it helps to have the real thing in your hand to test so I created a 3d model to send away for 3d printing.  There doesn't seem to be anything out there to create a 3d model from an equation so I had to write some software to do that.  I'll post that when I tidy it up and comment it properly.

I'm not made of money so the model is only 100mm x 100mm x 10mm (a volume of 100mL) with 20mm wide ripples that are 8mm deep.  By a stroke of luck, I happened to write the software is a way that easily calculates the volume of the model.  In this case the model is 80 mL.  As the bounding box of the model is 100 mL this means the volume of the 25 little cups is 20mL.  Each one holding 0.8 mL.

Rippled Drip Tray

I don't have the print yet, but it has been done and photos sent to me.  In theory this surface should hold 20 mL of liquid and covers an area of 100 square centimeters, so as a test I poured 20 mL of water on a flat surface and it spread to cover 180 square centimeters.  So already the ripple pattern has reduced the surface area by 45%

3D Printed Drip Tray Top

That may not sound like much, but the ripples can be made deeper.  If they were 3x times deeper (24mm) the surface would hold 60mL.  Once they get too deep though, you would need to make the ripples wider to make cleaning easier.  Changing the width of the ripples doesn't effect the volume that the surface would hold though.

3D Printed Drip Tray Top

In this demonstration I've shown the surface as a solid block with depressions.  In reality you'd use something like a polypropylene sheet moulded to this shape.  It would give an object shaped similar to an egg carton.

3D Printed Drip Tray Base

Anyway, this is just a thought that I wanted to explore.  Maybe it'll work out, maybe it won't.  Either way the process was enjoyable.

ABC Logo Lissajous Curve

Over the last couple of days I've seen a few people mention how similar the ABC Australian logo is to the new Disney Movies Anywhere service. I don't know much about the legal side of things, but I thought an explanation of why the ABC logo looks the way it does might be interesting.

The shape of logo is called a Lissajous figure or curve. The shape is generated by a parametric equation where the x and y coordinates are sinusoidal.  The frequency and phase relationship between the two equations for x and y determine the shape.  In the case of the ABC logo, the frequency of the y coordinate is 3 times that of the x coordinate and there is a 90 degree phase shift (I'll clarify this later) applied the y equation.

$$$x=cos(t)$$$ and $$$y=cos(3t+\pi/2)$$$

To make things clearer I've put together an animation. As the vertical bar sweeps across the screen it will intersect the x and y equations. The y coordinate is projected across and the x coordinate is projected across and up. The Lissajous figure is drawn where the project lines intersect.

Tracing a 3:1 Lissajous Curve x=cos(t)  y=cos(3t + $$$\pi$$$/2)

The phase shift is also very important to the shape. In the animation below you can see how the it changes as the phase shift is cycled across all possible values from 0 to $$$2\pi$$$.

Changing the phase relationship of a Lissajous Curve x=cos(t) y =cos(3t + $$$\delta$$$)

These curves aren't just a mathematical curiosity, they have a real world application. They used to be a very important tool for broadcast engineers. If two signals are feed into an oscilloscope (a tool that plots electrical waveforms) while it's in x-y mode, the Lissajous curve on the screen will reveal things about the signals.

The first thing to notice is that the number of horizontal and vertical lobes indicates the ratio of the frequencies. If the ratio of frequencies is rational (can be expressed as the ratio of two integers) the curve will be stationary. If not, it will slowly rotate like the second animation. If the two signal are meant to be locked together so that one is exactly 3 times the other like in the example above but the curve rotates, you know there's a problem. The rotation rate of the curve tells the engineer the deviation from the desired frequency. There are simple lookup tables like the one below that show what the curves should look like for a given phase shift and frequency ratio.

Frequency Ratios and Phase Differences

Earlier I said I'd elaborate on phase shift. The main thing to note is that you are working with two different frequencies.  1 degree of phase shift on one signal will take a different amount of time to 1 degree of phase shift on the other.  So it's important to not just note that there is a phase shift of 30 degrees, you have to specify what waveform you are referring to.  That's why a lot of the table results may be different from what you measure.  In a mathematical sense, it also makes a difference if you are talking about sine or cosine signal as one is a phase shifted version of the other.

Just to clear up another thing as well. The second animation is generated by plotting a waveform frame and then changing the phase an repeating this process. This is what makes it rotate. By chance though, this is exactly what you would see if the frequencies weren't locked together. A time varying phase is no different to making a small deviation to the frequency.

 

The code to generate the animations above is located here.  I did it as a quick project so didn't comment it.

 

Suburban Fulfilment Centre

A few weeks ago I was thinking about online grocery fulfilment and different ways of getting stock to customers faster. I had some ideas about the form factor of the facilities involved and thought I'd write about what I'm calling the Suburban Fulfilment Centre (SFC).

There are many important factors that add up to make a good online shopping experience, but when you strip away everything else, customers want a service that is fast, has a large range of products, and has reasonable fees. An important way to accomplish this is to do something that I call "tightening the loop". The time between a customer buying something and the stock being replenished and available for reorder needs to be as small as possible. It's important to have stock for customers to buy, but if you don't have a stock quickly flowing in to replace it you've failed.

Unlike regular parcel delivery, grocery shipments have some constraints that makes the process more challenging. Parts of the order need to be refrigerated, and some parts have a short shelf life. You can't just put a bottle of milk and some bananas in a box with some bubble wrap and ship it across the country in a cost effective manner. These constraints mean you need to have a supply of stock close to the final destination. If you're astute, you may have noticed that I just described a grocery store. Let's play with that idea.

What's really needed is a supermarket that's able to supply a much larger range, but keeping the online shopping model at the forefront of the planning. Around my local area a lot of 5 storey apartments are being built and I started to wonder if these could fill the roll. If an fulfilment centre with the exact same external appearance was built with a ground level drive-through, the only noticeable difference would be traffic to and from the centre. It would blend into the surrounding area and supplant current facilities that don't fit into the surrounds. To explore the idea, I selected a local set of apartments to study and run some numbers on.

Apartment Building

To further illustrate the idea, I've included some screenshots from StreetView of a storage company in Brisbane with a McDonald's wedged underneath it. The drive-though runs under the building and is similar to what I pictured for an ideal pick up location.

Ground Level Drive Through

Although I've been talking about a drive through for customers picking up orders, it would also serve as a loading dock for receiving stock and dispatching orders that get delivered directly to customers. Obviously there needs to be separation of different kinds of traffic for safety reasons, but there would be multiple drive-through lanes and when needed, one could be shut down and isolated for a delivery or dispatch.

Ground Level Drive Through

So how much space do we have to play with? The apartment shown above has a gross floor area of 419 m².

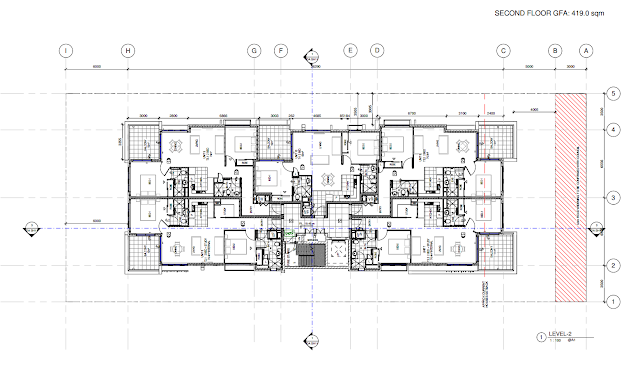Apartment Floor Plan

The height of the levels 1 to 4 is 11.2 meters. This gives us a volume of 4700 m³. But what does that actually mean? How much range can we fit in that volume?

Apartment Height

Let's look at the floor plan of a supermarket and do some visualisation exercises. It should be immediately obvious that there is a lot of unused floor space, what's not seen is that of the space that is utilised a lot of it is empty space. Next time you go shopping look at the displays and imagine what would happen if all the shelving suddenly vanished. How big would the pile of stock on the floor be? Typically shelves are utilised fully side to side, but vertically they might be only 70% full, and front to back they might be only 70% full on average. Therefore it's not outrageous to suggest that volumetrically, the shelves are only half full.

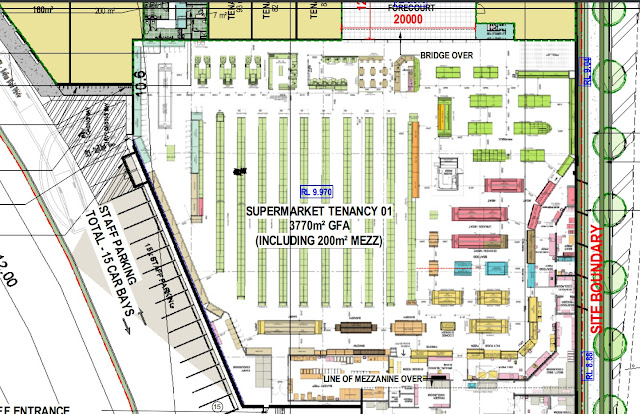Supermarket Floor Plan

How much does a supermarket hold though. Let's do some Fermi approximation.

10 aisles × 2 meters high × 1 meter wide × 15 meters long × half full = 150 m³

Let's say that the grocery department holds two thirds of all the stock in a store.  This means that in total a store holds 225 m³ of product.

Just as a sanity check, that's equivalent to the volume of 92 × 1.8 m high Australian pallets. From my experience that sounds about right to fill a store from empty.

Another important number to remember is that an average supermarket stocks about 15 thousand different items. This would mean that each item on average occupies about 15 L of space. That may seem wrong but some items need much more and some need a lot less, and remember this is the raw volume of the stock, not shelf space.

Let's look at how much space a purpose built fulfilment facility uses. The image below is of a supermarket dark store without customers. This makes it easier to fulfil online orders by staff manually picking individual orders.  As you can see though, not much of the facility is actually occupied. It's a giant waste of space. I can understand why they've done it though. It's a cheap and easy way to get started with online fulfilment without going all in automating the process. I'm still surprised that going all in is questioned. Amazon did it and look at how well it worked out for them.

Current Dark Store Layout

I keep talking about wasted space but what's the alternative? The system in the animation below is an automated tote storage and retrieval system by Dematic. There's wasted space in this example but the design can be optimised to use a lot more space of a building. It transfers the stock to a picking station where an operator assembles orders. This configuration is referred to as a goods to person solution, which means operators don't have to walk to assemble orders. It also reduces bending, reaching, and lifting.

The other important advantage of this is that each tote is traceable and for perishable food, its use by date is also known and action can be taken to clear the stock before it's wasted.

Dematic Multi-Shuttle System

Some items are so small that they may only fill part of a tote, in these cases a divider is used. In some cases items are too large to fit and will need to be stored in a bulk handling area. Over time a manufacturer may also alter their products to be tote friendly as it may offer a cost saving.

Dematic Multi-Shuttle System

Let's circle back to the concept of the suburban fulfilment centre with a 4700 m³ volume. Let's say only one third of it is used for a stock management system like the one by Dematic above, and of that third only one half of it is full. That's a raw stock volume of  783 m³. If each item takes up 15 L of space that means the building can hold about 52 thousand items. There's a lot of assumptions in my calculations and the number could be much higher or lower but I think it's worth investigating further. Especially when you take into consideration that extra items above what would normally be stocked in a supermarket would most likely take less space due to lower demand.

Each SFC doesn't need to hold the full range a service offers either. It may only need to hold 30 thousand core items and 20 thousand supplemental items. There may be multiple facilities reasonably close to each other that may hold different supplemental items and a few times a day small vans move stock between them.

The SFC would also be used to supply nearby retail spaces of the company with low demand items. that are a bit esoteric. Ask yourself if a supermarket really needs that many packets of black dye on the shelf or are they only there because that's how many come in a box. It's a waste of space and it's money sitting on the shelf.

Another consideration is the capacity of the drive through. If two lanes are open for 14 hours a day and a pick up take 2 minutes, that's 840 customers per day at capacity.  If they each take a 200 L trolley load that's 168 m³ of stock per day which the facility can easily hold.

I do actually have a serious reason for thinking about this problem. The less interaction staff have with stock the better. At the moment it's common practice for stock to arrive in store on a pallet like the one seen below. Think about that for a moment, at the warehouse people manually assemble these pallets and at the store people manually disassemble them. The only outcome of this process is people with injuries from a lifetime of manual labour. Finding meaningful replacement work for these people is important but I believe that a company has a moral obligation to minimise injuries where possible.

Pallet of stock

Finally to give you an idea of what the inside of what one of these facilities look like, the animation below is of a warehouse that does basically the same thing, only with pallets. Nothing I'm talking about is new, it's just a scaled down version of what's currently happening.

44m High, 12000 pallet, Jungheinrich High Rack Warehouse

I should point out that all ideas are my own and not those of my employer.  I've also purposefully used images publicly available online instead of using my own.

Supplemental documentation

Riveting Plywood to Metal

Today I'll give you a quick rundown of my experiment riveting aluminium to plywood.

2.8 mm Plywood Riveted to 1.4 mm Aluminium

If you've read my blog before you may know I like boxes and storage solutions.  I made some prototype storage boxes last year out of 19 mm pine and plywood, and since then they have been used quiet a lot.  The main problem I have with them is they are heavy, use more material than is really needed, and are complicated to make.  I wanted to simplify things and for inspiration I turned to an ammunition case that I have from 1958.  It's made from ply and is riveted together with metal edges.  All the components themselves are not specifically strong, but when assembled the case is rather sturdy.

Ammunition Box

I happened to find some brass rivets on AliExpress that are used for material, you may be wearing some now. Have a look at your jeans.  The type I purchased are called double capped, meaning they have flat rivets on both sides.  They consist of a cap and post that are pressed together.

Brass Rivet Cap

I ordered these because they were listed as 10 mm long.  I thought that this would mean I could join materials up to 10 mm (leaving room for compression of course).  Unfortunately I was mistaken. The length of the post is 10 mm but this only leaves 8.5 mm space for materials, and after compression of the rivets only about 5-6 mm are feasible.

Brass Rivet Post

.

Rivet Test Compression

For my test I planned to join some 6 mm ply to a piece of aluminium angle, but because the rivets are smaller than I planned I used 3 mm plywood.  Two 3 mm holes were drilled into the aluminium and the posts were inserted. A hole slightly larger (about 3.75 mm) was drilled in the ply, the caps inserted and the the rivets clipped together. For the final compression step no fancy tools were used. They were placed in a vice and I squashed the hell out of them.

The results speak for themselves. I think they look awesome and they will not budge.

Aluminium Side

The dark wood and brass look nice together gives the strength I need. I think I'm on to something.

Plywood Side

I'm not actually building a box in this post. This is just a test, and besides I don't think the size of box I want to make will work with 3 mm ply. I need slightly bigger rivets. So now we wait the standard 2 or 3 weeks for a shipment from China. :-(

There are plenty of designs for storage boxes that may be better than mine, but what I'm aiming for is a good strength to weight ratio box that can be easily assembled by people at home without exotic materials and tools.  The idea is that if you want a box you go and buy some ply and metal and use rivets you've purchased.